L’acqua nel terreno

Un materiale è permeabile se contiene vuoti continui  e ogni terra e roccia soddisfa a questa condiziona. Si ha così che l’acqua passa sia attraverso l’argilla che attraverso la ghiaia, ma tale fenomeno avviene con intensità completamente diverse. Più di un secolo fa Darcy studiò il flusso dell’acqua attraverso strati orizzontali di sabbia e stabilì che la velocità di flusso attraverso mezzi porosi è direttamente proporzionale alla perdita di carico e inversamente proporzionale alla lunghezza del percorso.

Darcy legò le varie grandezze con la ben nota relazione:

v = k i

nella quale v è la velocità di scarico, k il coefficiente di permeabilità o coefficiente di conducibilità idraulica e i è il gradiente idraulico o pendenza della linea piezometrica.

Questa relazione è valida per moto, nei canalicoli del terreno di tipo laminare. Terzaghi negli anni 1915-1925 ha dimostrato l’applicabilità della legge di Darcy a tutti i terreni.

Gli studi di Darcy hanno appunto indicato che la portata è proporzionale a h_L e a 1/L. introducendo la costante di proporzionalità k si ottiene:

Q = k A h_L / L                   v = Q / A = k i          i = h_L / L

Il coefficiente di permeabilità k  ha le dimensioni di una velocità e dipende dal mezzo poroso e dal fluido. Si ha infatti anche la permeabilità intrinseca o coefficiente di permeabilità k_p che è una caratteristica  solo del mezzo poroso, è indipendente dalle proprietà del fluido ed è legata al coefficiente di permeabilità k con la seguente relazione:

k = k_p ρ g / μ

nella quale ρ e μ sono la densità e la viscosità del fluido.

La densità e la viscosità dell’acqua nel terreno dipendono principalmente dalla temperatura e poiché le variazioni di temperatura nel terreno sono abbastanza piccole si può trascurare il loro effetto.

Sul coefficiente di permeabilità influiscono numerosi fattori. La permeabilità varia con la dimensione dei grani ed è molto sensibile alla quantità, al tipo e alle distribuzione delle frazioni fini; varia poi per uno stesso materiale in funzione della densità cioè al diminuire della densità aumenta la permeabilità. La permeabilità è influenzata dalla disposizione dei grani nel senso che le particelle possono essere più o meno stratificate e avere un orientazione prevalente; le frazioni fini possono essere disperse nel terreno o essere concentrate in modo non uniforme. I depositi naturali di terreno sono sempre più o meno stratificati e disuniformi nella struttura; ad esempio le terre che si sono depositate in presenza di acqua abbastanza spesso sono formate da una serie di strati orizzontali che variano per granulometria e permeabilità, cosicché generalmente questi depositi sono più permeabili in orizzontale che in verticale. Depositi eolici di sabbie e limi, invece sono spesso più permeabili in senso verticale che orizzontale a causa di vuoti verticali tubolari lasciati da piante ed erbe. In depositi ghiaiosi-sabbiosi si possono avere straterelli di ghiaia pulita che modificano radicalmente la permeabilità rappresentativa del deposito. Si possono pertanto avere variazioni di permeabilità in dipendenza delle modalità di formazione dei depositi.

Discontinuità di vario tipo presenti nei depositi influenzano grandemente la permeabilità; le fessurazione originate da varie cause nelle argille aumentano sensibilmente la permeabilità.

La permeabilità del terreno può essere misurata con prove in laboratorio e con prove in situ.

A causa dell’enorme campo di variazione della permeabilità nelle terre non vi è un unico metodo di laboratorio per tutti casi.

I tipi di prove generalmente comprendono:

a) il permeametro a carico costante fino ad un coefficiente di permeabilità dell’ordine di 10^-5 m/s;

b) il permeametro a carico variabile per k compreso tra 10^-5 e 10^-8 m/s.

per la determinazione di coefficienti inferiori a 10^-8 m/s è preferibile ricorrere a metodi indiretti quali le prove edometriche o di consolidazione.

Con il permeametro a carico costante si misura il volume di acqua che attraversa il campione di terra in un tempo t sotto l’azione di un carico costante h.

Il valore di k in m/s è dato dalla relazione:

k = CL/hAt

dove L è la lunghezza e A è la sezione del campione di terra, C il volume d’acqua raccolto nel tempo t e h il carico idraulico costante.

Il permeametro a carico variabile è invece usato per prove su materiali a media e bassa permeabilità, poiché le caratteristiche dell’apparecchiatura consentono di eseguire facilmente le misure del carico idraulico e del tempo per un largo campo di valori del coefficiente di permeabilità.

Il valore di k in m/s è dato dalla relazione:

k = 2,3 (aL / At) log₁₀ h₀ / h₁ (m/s)

dove a è la sezione del tubo di vetro, L la lunghezza del campione, A la sezione del campione, t il tempo, h₀ e h₁ il carico idraulico iniziale e finale.

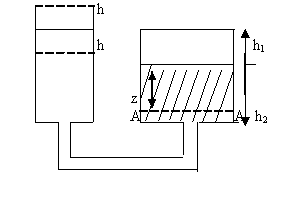
Per capire il comportamento del terreno è necessario stabilire una legge di interazione tra le varie fasi; tale legge è stata proposta nel 1923 da Terzaghi che l’ha definita principio delle tensioni efficaci.

Se allora consideriamo un elemento di terreno, le forze che agiscono in esso possono essere divise in due parti: quelle che sono trasmesse direttamente da grano a grano e quelle che agiscono attraverso il fluido che riempie i vuoti.

Le prime sono chiamate pressioni intergranulari o effettive o efficaci, le seconde pressione dell’acqua dei pori o pressioni neutre. Si consideri lo schema in basso:

si abbia un recipiente riempito per altezza h₂ con materiale granulare e per altezza (h₂ + h₁) con acqua. Al fondo del recipiente è attaccato un tubo collegato con un serbatoio nel quale l’acqua è allo stesso livello del recipiente con il materiale granulare; non vi è quindi alcun movimento dell’acqua. Sulla sezione AA alla profondità (h₁ + z) la pressione verticale σ è data da:

σ = h₁γ_w + zγ_sat

dove γ_w è il peso unitario dell’acqua e γ_sat il peso di volume del terreno saturo. Poiché σ dipende dal peso di tutto il materiale sovrastante viene chiamata pressione totale e Terzaghi ha mostrato che è legata alla pressione effettiva σ' ed alla pressione neutrale u dalla relazione:

σ = σ' + u

L’acqua sopra AA si estende attraverso vuoti continui per un’altezza z e in una massa continua sopra il materiale granulare per un altezza h₁. La pressione dell’acqua dei pori sul piano AA è perciò:

u = (h₁ + z) γ_w

La pressione effettiva è allora:

σ' = σ – u = z (γ_sat - γ_w )

Il termine (γ_sat - γ_w ) è chiamato peso di volume del terreno immerso e indicato con γ'. Si può perciò scrivere:

σ' = z γ'

Un’interpretazione fisica della pressione effettiva per i materiali granulari è stata data Skempton. Si considerino due grani di sabbia a contatto e sia A l’area totale del terreno soggetta al carico P. I due grani sono però a contatto su una piccola area A_s e le aree di contatto tra solido e acqua e tra solido e gas sono A_w e A_g. le pressioni nella fase solida, nella fase liquida e nella fase gassosa siano p_s, p_w e p_g. l’equilibrio delle forze normali all’area A è dato da:

P = p_s A_s + p_w A_w + p_g A_g

Dividendo tutto per A si ha:

P / A = σ = a p_s + X p_w + (1 – a – X) p_g

Essendo σ la pressione totale ed a, X e (1 – a – X) i rapporti tra l’area del solido, del liquido e del gas e l’area totale. X è evidentemente legato al grado di saturazione.

Se il terreno è saturo (1 – a – X) = 0 si può scrivere:

σ = a p_s + (1 – a) p_w

Nelle terre, per le condizioni che interessano i nostri problemi, il rapporto a è molto piccolo di modo che 1 – a è praticamente uguale all’unità. Tuttavia p_s cioè la pressione nell’area di contatto dei solidi, è molto elevata e probabilmente quasi eguale al carico di rottura del materiale solido in modo che il termine a p_s non si annulla, ma rappresenta la pressione effettiva σ'. Si può scrivere σ = a p_s + (1 – a) p_w  = σ' + u cioè la relazione di Terzaghi.

Comunque l’importanza del principio delle tensioni efficaci risiede nel fatto che il comportamento del terreno dipende dalla combinazione dei valori delle tensioni totali e neutrali e non dai loro singoli valori, cioè dipende dalle variazioni di σ' = σ – u.

Pertanto il principio della pressione effettiva riguarda sia i terreni a grana grossa che quelli a grana fine. Passiamo ora ad esaminare la situazione delle pressioni neutre ed effettive quando vi è un moto di filtrazione e consideriamo ancora la figura precedentemente osservata; se mantenendo fisso il livello dell’acqua nel recipiente, si abbassa di h il serbatoio, si ha un movimento d’acqua dal recipiente verso il serbatoio. Poiché la perdita di carico avviene tutta nel materiale granulare, la pressione neutrale al fondo del recipiente può essere espressa da u = (h₁ + h₂ – h) γ_w ; come si vede la presisone neutrale è diminuita di hγ_w rispetto a quella che si ha con acqua ferma. D’altra parte poiché la pressione totale al fondo del recipiente è determinato soltanto dal peso del terreno e dell’acqua al di sopra di esso, significa che è rimasta sempre la stessa e la pressione effettiva è aumentata di hγ_w . Questo incremento della presisone effettiva, dovuto al flusso dell’acqua attraverso i vuoti, è indicato come pressione di filtrazione. La perdita di carico tra la superficie superiore del materiale granulare e la profondità z è data da hz / h₂ ; il gradiente idraulico corrispondente è i = h / h₂ . La pressione di filtrazione può essere allora espressa con izγ_w e la pressione effettiva da σ' = zγ' + izγ_w . Se il serbatoio viene alzato di h rispetto al recipiente cosicché l’acqua fluisca dal serbatoio attraverso il materiale granular, la presisone dell’acqua alla base del recipiente aumenta di hγ_w ; quindi la pressione effettiva sul piano AA è ridotta a σ' = zγ' - izγ_w.

Se si aumenta il gradiente idraulico alzando il serbatoio, la pressione di filtrazione aumenta fino ad un valore zγ' per cui la pressione effettiva σ' si annulla. Ciò avviene quando zγ' – i_czγ_w = 0 e quindi:

i_c = γ' / γ_w

Questo è detto gradiente idraulico critico; in queste condizioni un terreno granulare non può sopportare alcun carico e le particelle di sabbia vengono a galleggiare ed a muoversi nell’acqua.

Il livello dell’acqua in un pozzo viene indicato con vari nomi, fra i quali superficie libera dell’acqua, livello della falda freatica, superficie freatica o alle volte semplicemente falda freatica. La falda freatica può essere anche definita come il livello al quale la pressione neutrale è uguale alla pressione atmosferica, cioè u = 0. Questa definizione è valida indipendentemente dal coefficiente di permeabilità. Sotto la falda freatica il terreno è praticamente saturo sopra dipende dalle condizioni climatiche, dalla granulometria del terreno e dalla distanza dalla falda freatica. I terreni a grana grossa sono parzialmente saturi anche immediatamente al di sopra della falda freatica, mentre i terreni a grana fine possono essere saturi anche per una notevole altezza.

Se in questi processi ci fosse solo la gravità allora il terreno sopra la falda freatica dovrebbe essere praticamente asciutto. L’acqua è però soggetta alla tensione superficiale, dovuta all’attrazione tra le sue molecole che si manifesta sulla superficie di separazione aria-acqua. La tensione superficiale combinata con l’attrazione tra l’acqua e la maggior parte delle sostanze solide costituisce una forza che si oppone alla gravità e tende ad attirare o trattenere l’acqua al di sopra della falda freatica. Questo fenomeno è chiamato capillarità. Infatti se infiliamo nell’acqua un tubo con un diametro di qualche decimetro di millimetro (tubo capillare) è possibile vedere come l’acqua risale.

Se indichiamo con T la tensione superficiale, con γ_w il peso specifico dell’acqua, con r il raggio del tubo, l’equilibrio richiede che: h_cπr²γ_w = 2πrT cosα cioè secondo la legge di Jurin:

h_c = ( 2 T / rγ_w ) cosα

Il valore di T diminuisce leggermente all’aumentare della temperatura. Alle temperature ambienti comuni è pari a circa 0,075 g/cm; per cui assumendo γ_w = 1 g/cm³ la relazione di prima diventa:

h_c ={ 0,15 / r (cm) } cosα

nel terreno al situazione è un po’ diversa; infatti i pori che compongono il terreno sono comunicanti tra loro tali da formare una specie di ragnatela di vuoti. Se questa “ragnatela” è invasa dall’acqua dal basso la parte più bassa comincia a saturarsi, mentre nella parte più alta solo i piccoli vuoti vengono invasi dall’acqua, i pori più grandi continuano a contenere aria. Al diminuire dei diametro dei grani e quindi dei vuoti, l’altezza di salita capillare aumenta; l’altezza h_c e all’incirca data da:

h_c = C_S / e D₁₀

in cui e è l’indice dei pori, D₁₀ è il diametro efficace e C_S è una costante empirica che dipende dalla forma dei grani e dall’impurità delle superfici e varia tra 0,1 e 0,5 cm² . tuttavia poiché la diminuzione di permeabilità associata alla diminuzione delle dimensioni riduce la velocità di salita capillare, l’altezza alla quale l’acqua salirà in un certo tempo ha un massimo per un certo diametro; ad esempio, in 24 ore l’altezza di capillarità è massima per le sabbie fini ed i limi.