Resistenza al taglio e  stato critico

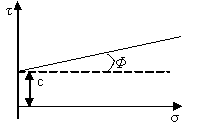
In genere il problema della resistenza è collegato al comportamento del terreno quando ha raggiunto grandi deformazioni e d’altro lato le deformazioni di una massa di terreno sono controllate dalle azioni reciproche tra le particelle che lo compongono e dalla loro mutua possibilità di scorrimento. In un primo momento possiamo quindi considerare che la resistenza sia almeno in parte controllata dalla resistenza al taglio sulle aree di contatto tra le particelle. Vedremo poi che tale resistenza notevolmente anche dall’incastro delle particelle e quindi è funzione della loro distribuzione strutturale.

La resistenza al taglio sulle aree di contatto tra le particelle è proporzionale alla forza che le spinge l’una contro l’altra e la possiamo pertanto considerare una forza di attrito.

Sui punti di contatto tra le particelle per alcuni tipi di terra si sviluppano delle forze di adesione che rientrano tra le azioni reciproche tra le particelle e quindi contribuiscono alla formazione della resistenza al taglio delle terre.

Coulomb già nel 1773 propose, per i mezzi granulari, la relazione tra la tensione di taglio e la tensione normale:

τ = α tgΦ

nella quale tgΦ esprime il coefficiente di attrito. Per i mezzi coerenti Coulomb propose che ad equilibrare il taglio oltre l’attrito figurasse anche una resistenza detta coesione che si manifesta anche a tensione normale nulla. La relazione di prima si riscrive nella forma:

τ = c + α tgΦ

rappresentata  in figura:

La svolta decisiva nello studio della resistenza al taglio si ebbe però solamente quando si scoprì che la differenza fondamentale tra le caratteristiche di resistenza al taglio e di comportamento delle sabbie e delle argille dipendeva non tanto dalle diverse proprietà d’attrito delle particelle quanto dall’enorme differenza di permeabilità.

La chiarificazione di questo fatto ebbe inizio con la scoperta da parte di Terzaghi del principio della pressione effettiva con la modifica della relazione di Coulomb nella forma:

τ = c' + (σ - u) tgΦ' = = c' + σ' tgΦ'        (4.1)

nella quale c ' e Φ' sono espressi in termini di pressioni effettive.

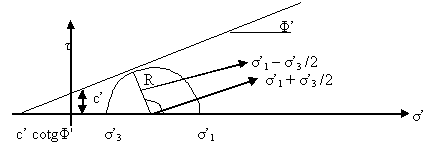
In questa nuova forma la relazione di Coulomb-Terzaghi ha assunto validità per una grande varietà di materiali e condizioni di carico.

Questa situazione di rottura è rappresentata nel piano τ, σ' da una retta i cui punti indicano stati tensionali a rottura; i punti al di sotto della retta rappresentano situazioni di particolare sicurezza rispetto alla rottura e quelli al di sopra situazioni irrealizzabili. Il problema venne ulteriormente chiarito associando alla relazione di Coulomb il criterio di rottura di Mohr τ = f(σ) secondo cui si ha rottura quando la tensione di taglio sul piano di rottura diventa una funzione della tensione normale a quel piano; questo criterio è espresso dalla relazione:

σ₁ – σ₃ / 2 = f [(σ₁ + σ₃)/2]

che indica che la rottura ha luogo quando il raggio del cerchio di Mohr delle tensioni (σ₁ – σ₃)/2 è funzione della semisomma delle tensioni principali maggiori e minori (σ₁ + σ₃)/2 cioè della distanza del centro di questo cerchio dall’origine.

Considerando la regola 5.1 essa può essere scritta in termini di pressioni effettive:

L’attrezzatura di prova fondamentale per lo studio del comportamento delle terre è quella per prove di compressione triassiale o cilindrica. Questa apparecchiatura è usata per determinare la resistenza al taglio. Di solito il provino è cilindrico con altezza paria a 2-2,5 volte il diametro. Nella prova triassiale il provino cilindrico di terra è racchiuso lateralmente da una sottile membrana di gomma fermata alle estremità da anelli pure di gomma; è separato dalla base e dal cappello di carico mediante piastre porose ed è posto in una cella cilindrica riempita di acqua. Alcuni collegamenti all’estremità del campione permettono il drenaggio dell’acqua o dell’aria dei pori del provino, la misura della pressione neutra e consentono di procedere alla saturazione del provino con l’applicazione di una presisone al fluido interstiziale.

Nella prova triassiale standard un provino cilindrico di terra è prima sottoposto ad una pressione isotropica  σ_r = σ_a = σ_c (fase di consolidazione), applicata mettendo in pressione l’acqua di cella (pressione di contenimento) e poi ad una pressione σ_a – σ_r applicata mediante una pressa a velocità di deformazione costante, fino ad arrivare alla rottura (fase di rottura). Poiché non vi sono tensioni di taglio sulle superfici del provino, la tensione di taglio σ_a e quella di contenimento σ_r sono le tensioni principali maggiore e minore σ₁ e σ₃, e l’incremento della tensione assiale σ_a – σ_r = σ₁ - σ₃ è indicato come tensione o sforzo deviatorico.

Le prove triassiali si distinguono in relazioni alle condizioni di drenaggio che si hanno durante ogni stadio:

a)  nelle prove senza drenaggio non vi è nessuna dissipazione di pressione dei pori né durante l’applicazione della pressione di contenimento σ₂ = σ₃  né durante l’applicazione della presisone verticale σ₁ - σ₃;

b)   nelle prove di consolidazione senza drenaggio viene permesso il drenaggio durante l’applicazione della pressione di contenimento σ₃ finché il campione è completamente consolidato sotto questa presisone, mentre durante l’applicazione della pressione verticale σ₁ - σ₃ non è permesso alcun drenaggio e si misura la pressione neutra;

c)   nelle prove con drenaggio, il drenaggio è possibile durante tutta la prova, si ha consolidazione completa sotto la pressione σ₃ , durante l’applicazione della pressione verticale σ₁ - σ₃ non si ha formazione di pressione neutra nel provino e si misurano le variazioni di volume del provino.

La suddivisione delle prove standard è legata principalmente alle condizioni di drenaggio. D’altro lato è evidente che queste possono avere notevole influenza se si ricorda l’enorme differenza di permeabilità tra terreni a grana grossa (elevata) e terreni a grana fine (bassa) e se si pensa al fenomeno della consolidazione esaminato con la prova edometrica (cap.4).

Con riferimenti a terreni a grana grossa qualunque variazione di pressione dell’acqua nel terreno si dissipa in tempi molto brevi.

Pertanto per questi terreni lo studio del comportamento dl materiale in campo statico può essere analizzato in condizioni drenate.

Con riferimento ai terreni a grana fine a causa della bassa permeabilità si possono avere tre situazioni possibili:

a)   nel caso di una costruzione realizzata in tempi brevi, per cui si possa fare l’ipotesi che la sovrapressione nutra prodotta dall’applicazione del carico si sia dissipata in entità trascurabile, è opportuno analizzare il problema delle deformazioni e di rottura in condizioni non drenate che corrispondo alla situazione iniziale di assenza di variazione di volume (volume costante). Si parla di analisi in condizioni non drenate o senza drenaggio;

b)   nel caso di uno scavo in terreno fine saturo, nelle zone adiacenti alle pareti si hanno delle variazioni negative o diminuzioni della presisone dell’acqua a causa dello scarico tensionale dovuto allo scavo; tali diminuzioni provocano un richiamo d’acqua dalle zone più distanti verso le pareti con rigonfiamento, rammollimento e riduzione della resistenza del terreno. La situazione più pericolosa si ha quindi ala fine del processo di filtrazione o meglio del processo di dissipazione delle sovrapresisoni neutrali e quindi in condizioni drenate;

c)   nel caso di un’opera costruita abbastanza gradualmente o in più fasi, per cui ci si può attendere un processo di consolidazione parziale, l’analisi può essere in condizioni non drenate, ma con la resistenza corrispondente alla consolidazione parziale.

Tenendo presente l’elevata permeabilità e quindi il fatto che le sovrapressioni si dissipano rapidamente, si può fare riferimento alle prove triassiali in condizioni drenate.

Iniziamo a considerare il comportamento di un provino di sabbia sciolta (bassa densità) e di un provino di sabbia densa (densità elevata) quando vengono portati a rottura nella seconda fase della prova triassiale.

Allo scopo studiamo gli andamenti dello sforzo deviatorico (σ₁ - σ₃) e dell’indice dei vuoti e, all’aumentare della deformazione triassiale ε_a con σ₃ eguale per le due sabbie.

La sabbia sciolta sottoposta allo sforzo deviatorico σ₁ - σ₃ aumenta di densità per arrivare a rottura; i grani si spostano per raggiungere una configurazione più stabile e l’indice dei vuoti iniziale e₀ si riduce fino a raggiungere un valore critico ed un corrispondente stato ultimo oltre il quale il materiale continua a deformarsi senza variazioni di volume e di resistenza. Si dice allora che la curva sforzi deformazioni è corrispondente ad un materiale incrudente.

La sabbia densa invece, sotto l’applicazione dello sforzo deviatorico all’inizio aumenta leggermente di densità con un corrispondente aumento di volume. Di conseguenza per arrivare a rottura occorre energia sia per il lavoro dovuto all’attrito legato agli spostamenti relativi delle particelle sia per il lavoro svolto per permettere l’aumento di volume contrastato dalle componenti normali.

La resistenza per arrivare alla rottura è quindi maggiore di quella della sabbia sciolta, la curva sforzi-deformazioni è corrispondente ad un materiale rammollente o dilatante e nella curva è chiaramente individuato un valore massimo detto rottura. Inoltre si vede che, superata la rottura, si ha una diminuzione di resistenza attribuibile alla diminuzione del grado di incastro e l’indice dei vuoti aumenta tenendo per grandi deformazioni verso il valore critico, cioè a quel valore che non varia con il procedere delle deformazioni.

Come è stato detto prima si utilizzano tre tipi di prove triassiali standard che si differenziano per le condizioni di drenaggio. Si hanno così le prove non consolidate non drenate e le prove consolidate drenate:

a)    Prove non consolidate non drenate (su terre coesive sature): come si è già detto, nella prima fase si applica una pressione di contenimento isotropa σ₃ tenendo il drenaggio chiuso e, nella seconda fase, si applica lo sforzo deviatorico σ₁ - σ₃ fino a rottura mantenendo il drenaggio chiuso. L’applicazione di σ₃ da luogo ad un eguale aumento della presisone neutrale u e quindi non avviene la consolidazione; con l’applicazione dello sforzo deviatorico si arriva a rottura praticamente a volume costante.

Pertanto eseguendo la prova su tre provini dello stesso campione variando σ₃ si trova uno sforzo deviatorico a rottura(σ₁ - σ₃)_f  pressoché eguale e nel diagramma τ-σ in termini di tensioni totali si hanno tre cerchi di dimensioni pressoché eguali poiché vi sono state variazioni di tensioni effettive eguali per i tre provini.

Le prove senza drenaggio vengono eseguite generalmente su terre coerenti sature o parzialmente sature; nel caso si terre sature queste prove sono eseguite su campioni indisturbati di argille, limi, argille organiche per misurare la resistenza che hanno strati naturali di terreno.

Se la resistenza al taglio è espressa in funzione della pressione totale normale nella relazione di Coulomb:

τ = c_u + σ tgΦ_u

nella quale c_u indica la coesione apparente, Φ_u indica l’angolo di resistenza al taglio in termini di pressione totale, si ha che in questo caso:

c_u = ½ (σ₁ - σ₃)

La coesione c_u che talvolta viene indicata con S_u, è detta resistenza al taglio in condizione non drenata o anche resistenza al taglio iniziale ed è usata nelle verifiche di stabilità eseguite in termini di tensioni totali e che, per questi tipi di terreno, sono conosciute anche come verifiche con Φ_u = 0 o verifiche in condizioni non drenate.

La resistenza aumenta con la pressione della cella poiché la compressione dell’aria dei vuoti permette un aumento delle pressioni effettive. Tuttavia l’aumento di resistenza diventa sempre più piccolo man mano che l’aria viene compressa o va in soluzione e cessa quando le sollecitazioni sono sufficientemente grandi da determinare la saturazione e quindi Φ_u si avvicina a zero.

La linea di inviluppo alla rottura espressa in termini di tensioni totali non è quindi lineare ed i valori di c_u e Φ_u  devono essere stabiliti per campi delle tensioni ben determinati.

Alcune argille diminuiscono di resistenza se sono assoggettate a rimaneggiamento

b)   Prove consolidate non drenate con misura della pressione neutra su terre coesive sature: le prove con consolidazione senza drenaggio, con misura della pressione dei pori su terre coerenti sature, sono eseguite su campioni indisturbati e su campioni rimaneggiati per determinare i valori di c' e Φ' in termini di pressioni effettive e di c_u per diverse pressioni si consolidazione .

Nella prova standard il campione viene lasciato consolidare sotto una pressione σ₃ della cella e in tali condizioni le tre tensioni principali sono eguali; il campione viene poi portato in assenza di drenaggio applicando una pressione assiale σ₁ - σ₃. Nella seconda fase durante l’applicazione della pressione verticale senza drenaggio viene misurata la pressione neutra. Nell’argilla consolidata normalmente si ha un aumento di pressione neutra durante l’applicazione dello sforzo deviatorico, mentre con l’argilla sovraconsolidata dopo un iniziale leggero aumento si ha una diminuzione di pressione neutra. Per argille consolidate normalmente la linea di inviluppo è retta con c'=0 e con il valore di Φ' dipendente dal tipo di terra. L’inviluppo dei cerchi di argille sovraconsolidate per il campo di tensioni inferiori alla pressione di consolidazione, indica generalmente una coesione c' ed un angolo di attrito interno Φ'.

c)   Prove consolidate drenate: più raramente si eseguono le prove triassiali consolidate drenate; con queste prove la seconda fase deve essere condotta così lentamente da non sviluppare pressioni neutre e sono perciò necessari tempi variabili da giorni a settimane. Durante queste prove l’argilla normal consolidata diminuisce di volume mentre l’argilla sovraconsolidata si espande ed aumenta di volume.

Nelle prove di taglio diretto la rottura viene raggiunta nel provino provocando il taglio secondo un piano prestabilito e lo stato tensionale è di tipo edometrico. In questa classe rientrano vari tipi di prove, ma la più usata è quella eseguita con lo strumento di Casagrande, costituito da due telai sovrapposti di cui uno è scorrevole rispetto all’altro; il provino può essere a base quadrata o cilindrico. Il provino è contenuto nei due telai e si applica ad esso uno sforzo di compressione N e attraverso un telaio uno sforzo orizzontale T. La terra si rompe per un valore di T secondo il piano di separazione tra i due telai. Conoscendo N e T e la sezione A del campione si possono determinare i corrispondenti valori σ = N / A e di τ = T / A con A considerata costante nel corso della prova. Ripetendo la prova per vari campioni con diversi valori di N si ricavano i corrispondenti valori di rottura τ_f (sforzo di taglio alla rottura) e quindi si può tracciare la τ_f = c + σ tgΦ.

La prova viene condotta a velocità di scorrimento orizzontale controllata misurando il valore di T al crescere dello spostamento. Si può quindi tracciare il diagramma τ-spostamento per diversi valori di N e quindi determinare il valore massimo di τ_f. In questa prova ci sono anche dei difetti, quali la distribuzione disuniformi delle tensioni, l’impossibilità di controllare il drenaggio e la diminuzione della superficie di taglio durante la prova.

Attualmente una prova che sta dando numerosi risultati è quella di taglio semplice. Il provino circolare è all’interno di una membrana di gomma rinforzata esternamente con anelli metallici; la membrana permette deformazioni di taglio γ, ma impedisce le deformazioni orizzontali. Il campione poggia su una pietra porosa, ed è quindi possibile controllare il drenaggio ed eventualmente misurare la pressione neutra. Lo stato tensionale, come nella prova di taglio diretto , è del tipo edometrico.

I valori della resistenza cui si è fatto riferimento nel discutere le varie prove triassiali e di taglio diretto riguardano il valore massimo della resistenza al taglio.

Quando la prova è prolungata fino a raggiungere valori molto elevati di deformazione, si osserva una diminuzione della resistenza fino al raggiungimento di un valore indicato come resistenza residua, che nel caso di materiali a grana grossa abbiamo indicato come resistenza a volume costante.

Per determinare la resistenza residua ed i valori di Φ_r corrispondenti si può ricorrere all’apparecchio di taglio diretto e a quello di taglio torsionale; nella prova di taglio diretto, per arrivare ad una stabilizzazione dei valori della resistenza residua, può essere necessario eseguire 15-20 cicli di andata e ritorno della deformazione di taglio.

La diminuzione della resistenza di picco fino a quella residua nelle argille è legata principalmente al fenomeno di dilatanza, al riorientamento delle particelle nella zona di rottura e della distruzione di eventuali legami di cementazione.

La differenza tra la resistenza di picco e quella residua cresce all’aumentare del grado di sovraconsolidazione, del contenuto di argilla e dell’indice di plasticità.

La resistenza residua è indipendente dalla storia tensionale dell’argilla e ciò sembra sia legato ad una rottura progressiva dei legami di adesione fra le particelle e ad un riorientamento delle particelle verso una disposizione parallela.